One of the things you can do with a matrix is factorize it.
The Jupyter Notebook for this little project is found here.
Singular Value Decomposition (SVD)
SVD decomposes ( matrix) into 3 parts:
- is a matrix of size
- is a diagonal matrix whose
diagonal entries are known as the singular values - is a matrix of size
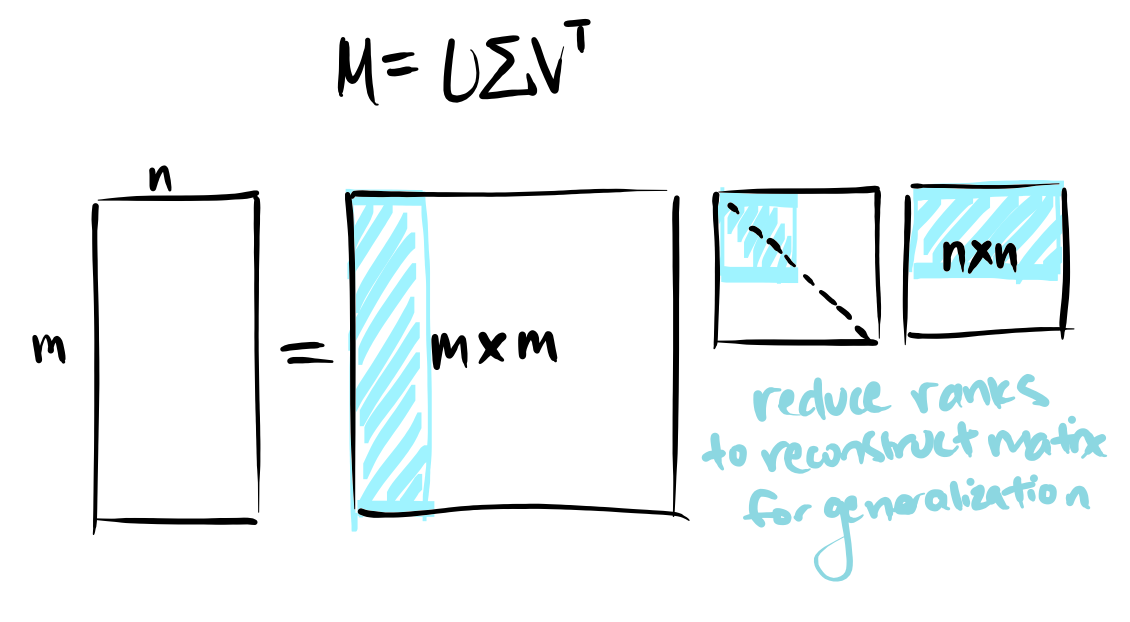
- rank refers to the maximum number of linearly independent vectors in a matrix
Once the matrix is factorized, one then reduces the rank of the matrix. This is done by removing singular values from the decomposed matrices (ie. keeping only the blue parts in the above figure) and then reconstructing/recombining the matrix. This loss of information from removing singular values will then produce a generalized matrix for which we can learn, compare with the original matrix, and make predictions from.
Singular value decomposition is essentially trying to reduce a rank R matrix to a rank K matrix.
- What is an intuitive explanation of singular value decomposition (SVD)? (Jason Liu, 2016)
SVD in Python
Searching for how to run SVD in Python, I come across two implementations numpy.linalg.svd and scipy.linalg.svd.
import numpy as np
U, s, V = np.linalg.svd(M)
import scipy.linalg
U, s, V = scipy.linalg.svd(M)
According to “Why both numpy.linalg and scipy.linalg? What’s the difference?”, scipy.linalg is a more complete wrapping of Fortran LAPACK using f2py.
SVD on the full matrix
The size of the document-word count matrix from yesterday is . When we run SVD on the full matrix, the job fails. The matrix is too big.
SVD on a subset of the matrix
Here we take a subset (with only 10,000 documents and 100 words) and deconstruct the matrix with SVD:
import scipy.linalg
# Subset M
M = M[:10000, :100]
# Run SVD
U, s, Vh = scipy.linalg.svd(x)
# U.shape, Vh.shape, s.shape
#> ((10000, 10000), (100, 100), (100,))
Next we plot the singular values of :
import seaborn as sns
f, ax = plt.subplots(figsize=(15,4))
sns.pointplot(y=s, x=list(range(1,len(s)+1)))
ax.set(xlabel="singular values", ylabel="eigenvalue")
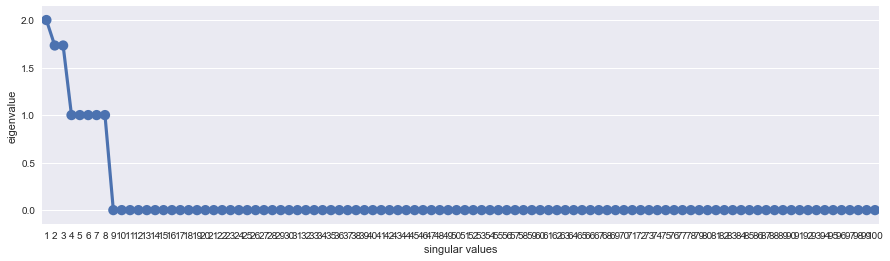
There is information in the first 8 singular values.
Finally we reconstruct the matrix with the top 8 singular values:
numSV = 8
U = U[:,:numSV]
Vh = Vh[:numSV,:]
s = s[:numSV]
# U.shape, Vh.shape, s.shape
#> ((10000, 8), (8, 100), (8,))
# Reconstruct the original matrix
reconstructed = np.dot(np.dot(U,np.diag(s)), Vh)
Future work
SVD runs on the smaller matrix, but errors on the full one. In the future work, I’ll investigate how matrix decomposition is done with bigger matrices.